指数平滑模型
一 定义:时间序列是指将某一现象所发生的数量变化,依时间的先后顺序排列,以揭示随着时间的推移,这一现象的发展规律,从而用以预测现象发展的方向及其数量。
二 时间序列分类:水平型时间序列、季节型时间序列、循环型时间序列、直线趋势型时间序列和曲线趋势型时间序列。
1)水平型:又称为稳定型时间序列或平稳型时间序列。这是因为这种数据走势无倾向性,不增不减,总是在某一个水平上下波动,同时这种波动也是无规律性。如日用必需品的销售量,某耐用消费品的合格率、返修率等等。
2)季节型:序列的走势按时间发生周期性的变化,即在某段时间后序列值逐步向上,到顶峰后逐步向下,后来又逐步向上,周而复始。如与季节气候有关的季节型商品的销售量等。
3)循环型:循环型时间数列的走势也呈周期性变化,但他不是在一个不变的时间间隔中反复出现,且每一周期长度一般都有若干年。通常呈循环型时间数列的有期货价格、商业周期等等。
4)直线趋势型:序列显示出一定的倾向性,即在一段时间内呈现逐步增加或逐步减少的趋势。如某段时间的人均收入、商品的销售量等等。
5)曲线趋势型:序列走势也具有倾向性,会逐渐转向,包括顺转和逆转,但不发生周期性的变化,时间序列后序值增加或减少的幅度会逐渐扩大或缩小。如某商品从进入市场到被市场淘汰的销售量变化等。
三 时间序列组成成分:一个典型的时间序列可分为四个部分:趋势、季节、周期和随机波动。趋势是数据在一段时间的逐渐向上或向下的波动。季节是数据自身经过一定周期的天数,周数,月数或季度数的不断重复性。周期为数据每隔几年重复发生的时间序列形式,他们一般与经济周期相关,并对短期经营分析与计划起重要作用。随机波动是由偶然、非经常性原因引起的数据变动,它们没有可识别的形式。
四 时间序列分析方法:时间序列分析力求以历史数据为基础预测未来,其中包含很多种预测模型:移动平均法、指数平滑法、ARIMA法、季节解构法等。在实际的应用中选择哪种模型预测取决于:预测的时间范围;能否获得相关数据;所需的预测精度;预测预算的规模;合格的预测人员等。
1.1 算法摘要
指数平滑是进行趋势分析和预测时常用的一种方法,适用于拟合与预测没有明显趋势和季节波动的序列。指数平滑在对中短期经济发展趋势中,不丢弃过去的数据,并给予逐渐减弱的影响程度,以与预测未来几期的发展。
所以说,指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法,它是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测,其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。
1.2 算法原理
指数平滑它是利用修匀技术,削弱短期随机波动对序列的影响,使序列平滑化,从而显示出长期趋势变化的规律。用序列过去值的加权均值来预测将来的值,序列中近期的数据被赋以较大的权重,远期的数据被赋以较小的权重。理由是一般情况下,某一变量值对其后继行为的影响作用是逐渐衰减的。
常用的指数平滑模型包含了四种类型:单指数平滑模型、Holt-Winter无季节性模型、Holt-Winter加法模型、Holt-Winter乘法模型。
单指数平滑模型,即一次指数平滑,表达式及预测公式为:
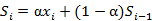 ,
,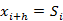
无季节模型,即二次指数平滑,表达式及预测公式为:
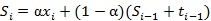
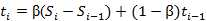 ,
,
加法模型,即三次指数平滑累加,表达式及预测公式为:
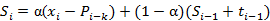
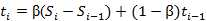
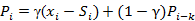 ,
,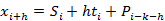
乘法模型,即三次指数平滑累乘,表达式及预测公式为:

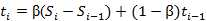
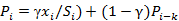 ,
,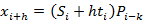
其中参数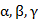 的值都位于[0,1]之间,可多实验几次已达到最佳效果;同时
的值都位于[0,1]之间,可多实验几次已达到最佳效果;同时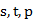 的初始值选取对于算法整体影响不是特别大,通常取值为:
的初始值选取对于算法整体影响不是特别大,通常取值为: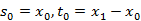 ,加法模型P=0,乘法模型P=1。
,加法模型P=0,乘法模型P=1。
根据指数平滑模型得到了预测的表达式,下一步就要对指数平滑的趋势进行调整。在一段时间内收集到的数据所呈现的上升或下降趋势将导致指数预测滞后于实际需求。通过趋势调整,添加趋势修正值,可以在一定程度上改进指数平滑预测效果。调整后的指数平滑法的公式为:
包含趋势预测(YITt)=新预测(Yt)+趋势校正(Tt)
进行趋势调整的指数平滑预测有三个步骤:
1)计算第t期的简单指数平滑预测(Yt);
2)计算趋势。公式为:Tt=(1-b)Tt-1+b(Yt-Yt-1),其中Tt表示第t期经过平滑的趋势;Tt-1表示第t-1期经过平滑的趋势;b表示选择的趋势平滑系数;Yt是对第t期简单指数平滑预测;Yt-1表示第t-1期简单指数平滑预测。
3)计算趋势调整后的指数平滑预测值(YITt),计算公式为:YITt=Yt+Tt。
二算法背景指数平滑是布朗(Robert G.Brown)提出的,他认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理的顺势推延;他认为最近产生的过去态势,在某种程度上会持续影响到最近的一段时间,所以将较大的权数放在最靠近近期的期数上。
三相关应用指数平滑是进行趋势分析和预测时常用的一种方法,适用于拟合与预测没有明显趋势和季节波动的序列。
四参考资料1 安鸿志,时间序列分析,上海:华东师范大学出版社,1992
2 何书元,应用时间序列分析,北京:北京大学出版社,2003.9
3 Shumway R H and Stoffer D S ,Time Series Analysis and Its Application.New York:Springer-Verlag,2000
4 Hamilton J. Time Series Analysis.Princeton University Press,1994(中译本:刘明志译.时间序列分析,中国科学出版社,1999)
5 马克威分析系统使用教程,http://www.tenly.com
五实例在进行指数平滑模型分析前,可以利用统计图形,对序列的走势、周期或平稳性做出一个大致的判断,以便对模型的参数设置有一个比较正确的最初判断,把握分析的方向。下面给出指数平滑算法的数据:
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | …… |
| X | 4.77 | 3.37 | 6.14 | 3.95 | 3.56 | 4.23 | 4.31 | 4.71 | 5.69 | …… |
| 编号 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 |
| X | 3.89 | 4.6 | 4.47 | 3.64 | 4.34 | 5.18 | 6.14 | 3.24 | 4.9 | 3.05 |
根据指数平滑的计算得到的结果为:
预测的四期值分别为:X102=4.6508;X103=4.8803;X104=4.996;X105=4.9909;计算的结果残差平方和为:SSE=74.58,各个参数分别为:Alpha=0;Delta=0;Gamma=0.8。
六输入输出输入变量类型:整型、浮点型(注:输入数据可分为周期性和非周期性两种;具有周期性质的序列以及相应的年、月,非周期性数据t>=1即可。两者都不处理数据有缺失情况。)
输入数据尺度:标量型、有序型
输出结果:预测的结果
七相关条目移动平均法、修匀技术、随机波动
八优缺点优点:所需数据资料少,就可以预测出来所需要的结果,指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法,兼容了全期平均和移动平均所长,不舍弃过去的数据,但是仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数是通过计算指数平滑值,配合一定的时间序列预测模型对现象的未来进行预测。
缺点:赋予远期较小的比重,近期较大的比重,所以只能进行短期预测。