马克威K-L信息量
马克威操作说明
以数据文件“马克威通用数据2.mkw”为例，演示K-L信息量算法的操作说明。
（1）首先，在工作区，打开建模分析工作流“高级统计”→“指标分析”→“时差相关分析”；
（2）接着选择数据源；
（3）然后设置算法的参数；
（4）主要的操作步骤如下：
1）选择数据源；
2）变量选择：
基准指标：表示用于分析的基准指标列表。
被选指标：表示用于分析的被选择指标列表。注：进行时差相关分析的指标序列均为采用季节调整并去掉不规则要素后的序列。
延迟数：指定最大延迟数，最大延迟数取值为1到12之间的整数，默认为12。当指定最大延迟数为L时，则使被选择指标超前或滞后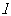
期（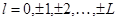
），计算它们的相关系数。
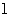取负数时表示先行，取正数时表示滞后，等于0时表示同步。
参数设置如下所示，选取GDP为基准指标，CPI为被选指标，延迟数设置为12：
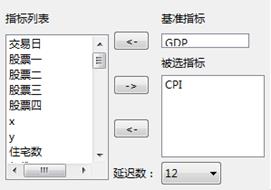
（5）输出结果：
K-L信息量：
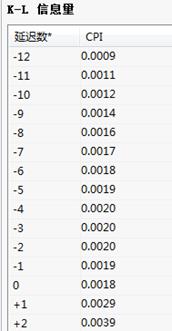
K-L信息量分析结果：
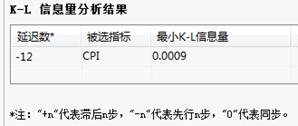
（6）结果说明：
K-L信息量表给出了被选指标的先行和滞后的相关系数；同时K-L信息量分析结果给出了被选指标的最大时差相关系数。
数据要求
输入变量类型：要求数值型变量；如：整型、浮点型、日期型；
注：进行K-L信息量分析的指标序列均为采用季节调整并去掉不规则要素后的序列。
算法用途
K-L信息量被运用到经济分析中，用来选择景气指标。将K-L信息量用于选择景气指标的实际计算中，也要以一个重要的、能够敏感地反映当前经济活动的经济指标作为基准指标。
在实际应用中选择好基准指标后，对任意选取的经济指标相对基准指标前后移动若干个月，计算K-L信息量的值；若值越小，说明真实概率分布与模型概率分布越接近，对应的移动月数就是该指标的延迟月数。
算法原理
K-L信息量，用以判定两个概率分布的接近程度。其原理是以基准序列为理论分布，备选指标为样本分布，不断变化被选指标与基准序列时差，计算K-L信息量；K-L信息量最小时对应的时差数确定为备选指标的最终时差。
结果与解释
输出结果：
K-L信息量：给出被选指标的先行和滞后的相关系数；
K-L信息量分析结果：给出被选指标的最小K-L信息量。