马克威移动平均模型
马克威操作说明
以数据文件“马克威通用数据2.mkw”为例,演示移动平均模型算法的操作。数据为记录了四支股票293个交易日的有关数据,试用移动平均模型来预测股票二在其后若干交易日的数据。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“时间序列”→“移动平均模型”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要的操作步骤如下:
1)选择数据源;
2)变量选择:
已选变量:表示用于分析的变量列表。
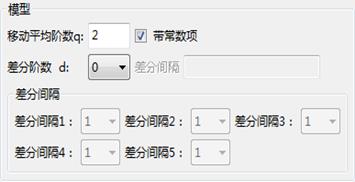
移动平均阶数:指定移动平均阶数q,要求为非负整数。
带常数项:指定移动平均模型是否包含常数项。
差分阶数:指定差分阶数d,要求为非负数。计算自相关函数,使其很快衰减的d就是序列达到平稳的阶数。
差分间隔:指定每次差分的间隔。
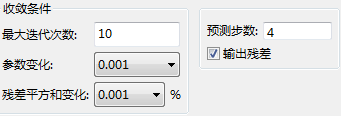
收敛条件:设置结束迭代的收敛条件。
最大迭代次数:用于控制计算。当算法迭代到最大迭代次数时,如果此时算法未收敛,则跳出循环。
参数变化:用于控制计算的精度,在此处设置的值越小,计算精度越高。
残差平方和变化:用于控制计算的精度。在此处设置的值越小,计算精度越高。即当原序列与拟合序列的残差平方和小于0.001%时,跳出循环。
预测步数:即预测的时间长度,已知时间序列,预测后面的n个单位时刻的行为,则即为预测的步数。
3)选择需要输出的结果
输出残差:选择是否输出残差表。
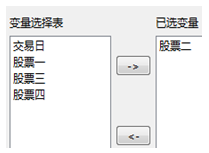
参数设置如下所示,变量选择“股票二”,移动平均阶数为2阶:
(5)输出结果:
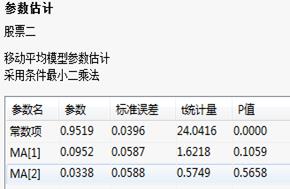
参数估计表:
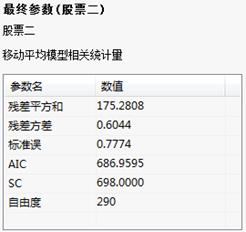
最终参数:
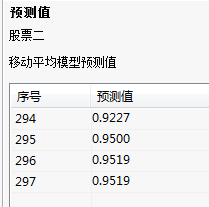
预测值:
(6)结果说明:
参数估计表:给出了参数检验的结果,除常数项的系数显著性为0.0000,统计意义显著外,其余各项的显著性大于0.05,不能拒绝原假设,即认为系数不显著。
最终参数表:给出的是模型的拟合优度统计量。AIC越小的模型相对较好。预测值表:给出了294-297,4个交易日的预测值;标准误差越小越好。
数据要求
输入变量类型:整型、浮点型
输入数据尺度:标量型
算法用途
移动平均模型是一种简单平滑预测技术,用一组最近的实际数据值来预测未来趋势的一种常用方法,移动平均法适用于近期预测。当需求既不快速增长也不快速下降,且不存在季节性因素时,移动平均法能够有效的消除随机波动,提高预测的精度,减少误差。
算法原理
移动平均法的基本原理可以归纳为:通过移动平均、周期(及其整数倍)与移动平均项数相等的周期性变动,消除时间序列中的不规则变动和其他变动,从而揭示出时间序列的长期趋势。
移动平均模型可以看做是自回归模型的推导模式;自回归模型理论上可以表示任意经济变量的时间序列,但包含的参数过多,不好估计;为了简化参数估计的难度,推导出移动平均模型。移动平均模型认为系统当前值与其以前时刻的自身值无关,而与在此之前进入系统的扰动(噪音)存在一定的关系。这一关系可表示为:
考虑无穷阶自回归过程和时间推迟一期的过程:
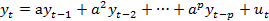
其中系数a是待估参数,p是滞后期限的数目,ut为随机误差项(白噪声)
推导至q阶的移动平均过程得到如下形式的随机过程:

结果与解释
输出结果:
参数估计表:给出了参数检验的结果,系数显著性小于0.05,统计意义显著,显著性大于0.05,系数不显著。
最终参数表:给出的是模型的拟合优度统计量。AIC越小的模型相对较好。
相关系数表:给出参数的相关系数,数值较大则存在多重共线性。
预测值表:给出预测值。
预测图: 拟合值和预测值用不同颜色的线表示出来(预测值见于预测图最右端)。