马克威误差修正模型
马克威操作说明
以数据文件“马克威通用数据2.mkw”为例,演示误差修正模型算法的操作。
(1)首先,在工作区,打开建模分析工作流“高级统计”→“协整分析”→“误差修正模型”;
(2)接着选择数据源;
(3)然后设置算法的参数;
(4)主要的操作步骤如下:
1)选择数据源;
2)变量选择:
检验变量列表:待检验的变量。
外生变量列表:选入对要进行检验的变量有影响的变量,即外生变量,
要求为浮点型变量。
滞后阶数:输入滞后阶数,要求为非负整数。
协整方程个数:输入协整方程的个数,要求为非负整数。
有无常数项和趋势:根据趋势项的性质,分为“无决定趋势”、“线性决定趋势”、“二次决定趋势”三大类,共五种模型。要求在其中选定一个,对常数项和趋势做出设定。
设置好参数如下所示:
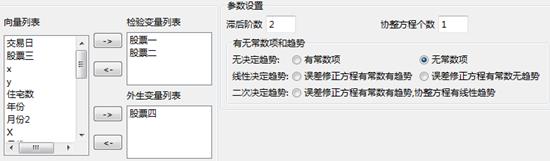
(5)输出结果:
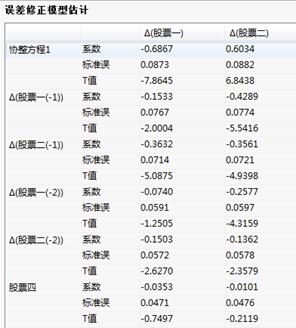
误差修正模型:
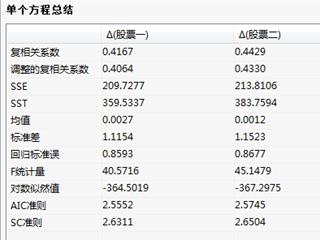
单个方程总结:
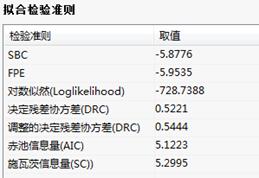
拟合检验准则:
(6)结果说明:
误差修正模型表:给出了协整分析中的各变量的统计量;单个方程总结和拟合检验准则给出了变量的统计量以及检验的不同准则。
数据要求
输入变量类型:要求数值型变量;如:整型、浮点型
算法用途
在现实经济中变量很少处于均衡位置,我们利用变量间的长期均衡关系,测算出协整方程的误差修正,利用记录值的变化对该误差进行回归所得的就是误差修正模型。
系统使用的是约翰逊的约束极大似然算法,并且要区分是否含有常数项和趋势项。
算法原理
根据格兰杰定理可知:如果若干非平稳变量存在协整关系,则这些变量必有误差修正模型表达式存在。而简单的模型表达式可以表示为:
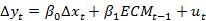
其中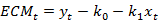 为非均衡误差;
为非均衡误差;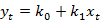 表示
表示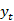 和
和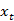 的长期关系,
的长期关系,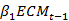 是误差修正项;
是误差修正项;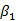 是修正系数,表示误差修正项对
是修正系数,表示误差修正项对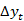 的修正速度。
的修正速度。
结果与解释
输出结果:
协整关系矩阵估计:给出协整变量的系数矩阵估计;
误差修正模型估计:给出协整分析的误差修正模型统计量;
单个方程总结:给出协整分析的单个方程总结统计量;
拟合格检验准则:给出变量的统计量。