马克威变量相关分析
马克威操作说明
（1）以数据文件“马克威通用数据1.mkw”为例，演示变量相关分析算法的操作。首先，在工作区内，打开建模分析工作流：“基础分析→相关分析→变量相关分析”，接着选择数据源，然后设置算法的参数，最后点击运行按钮。
其中各类参数的含义为：
缺省值排除：选择缺失数据的处理方式，包括成对排除和整行排除两种方式：
成对排除：即参与计算的变量若有缺失，则剔除与之对应的另一个变量，即一次排除一对变量。
整行排除：即一行中若有缺失值，则剔除一行数据，而不考虑有缺失值的变量是否参与计算。
显著检验：包括单尾检验和双尾检验两种。
分析方法：选择所使用的相关分析方法。
选择变量“sodium1”和“sodium2”进行变量相关分析。具体的参数设置如下所示：
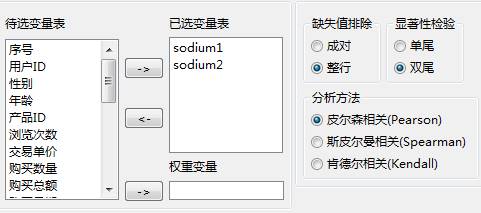图 0-1 变量相关分析-属性设置
（2）输出结果
双击“运行”节点，输出结果：
图 0-2 变量相关分析-树形结果列表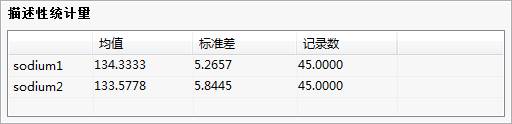
图 0-3 变量相关分析-描述性统计量
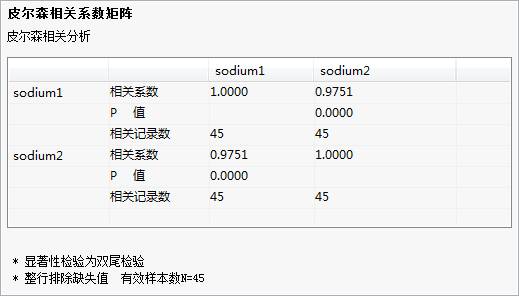图 0-4 变量相关分析-皮尔森相关系数矩阵
（3）结果说明
从皮尔森相关系数矩阵可以看出变量sodium1和变量sodium2有很高的相关性。这是因为它们的相关系数为0.9751，同时P值远小于0.05。所以表明这两个变量之间的相关系数具有统计学的意义。
数据要求
输入变量类型：整型、浮点型
输入数据尺度：标量型、名义型、有序型
算法用途
反映两变量间的简单相关关系。
算法原理
相关系数用于计算反映两变量间的简单相关，包括两个连续变量间的相关和两个等级变量间的秩相关。计算相关系数的方法有三种：分别是皮尔森相关（Pearson）、斯皮尔曼相关（Spearman）、肯德尔相关（Kendall）；
皮尔森相关（Pearson）：也称为积矩相关系数或动差乘积相关系数，计算Pearson相关系数，适合于变量是连续型变量（又称等间隔测度变量）。
斯皮尔曼相关（Spearman）：计算Spearman相关系数，适合于有序变量或不满足正态分布假设的等间隔数据。
肯德尔相关（Kendall）：计算Kendall相关系数，适合于有序变量或不满足正态分布假设的等间隔数据。
结果与解释
输出结果
皮尔森相关系数矩阵：相关系数为r，当r＝0时，表示不存在线性相关；当0＜r≤0.3时，为微弱相关；当0.3＜r≤0.5时，为低度相关；当0.5＜r≤0.8时，为显著相关；当0.8＜r<1时，为高度相关；当r＝1时，为完全线性相关。